Chapter 7
Single Photon Energy Loss and Resolution

In order to compare the number of single photon events to an analytical prediction for the single photon process, e⁺e^-Ž n[`(n)]g, it is necessary to fully understand the effects of the energy loss incurred by the photon due to the coil. Since the single photon energy spectrum at Ös ť M_Z⁰ falls off sharply, an accurate representation of the correction for the energy loss and resolution is essential. To compare directly with the prediction for e⁺e^-Ž n[`(n)]g, this analysis focuses on understanding the energy loss, correcting for the loss, and selecting events based on the corrected energy. This chapter discusses the single photon energy loss and resolution in the context of the single photon counting measurement presented in this thesis.

7.1 Single Photon Energy Loss and Resolution

Corrections for the energy loss, DE_g, are determined from the Monte Carlo simulation and checked for consistency using the single electron events. Here, DE_g is due primarily to energy losses in the coil and is defined as DE_g = E_g^corr - E_g^raw. The energy corrections are determined from the Monte Carlo simulation of e⁺e^-Ž n[`(n)]g by comparing the Monte Carlo energy, E_g^four vec., where E_g^corr = E_g^four vec. to the simulated energy observed in the detector, E_g^raw, where E_g^raw = E_g^obs. as follows,

DE_g

E_g^corr-E_g^raw =E_g^four vec.-E_g^obs.

(7.1)

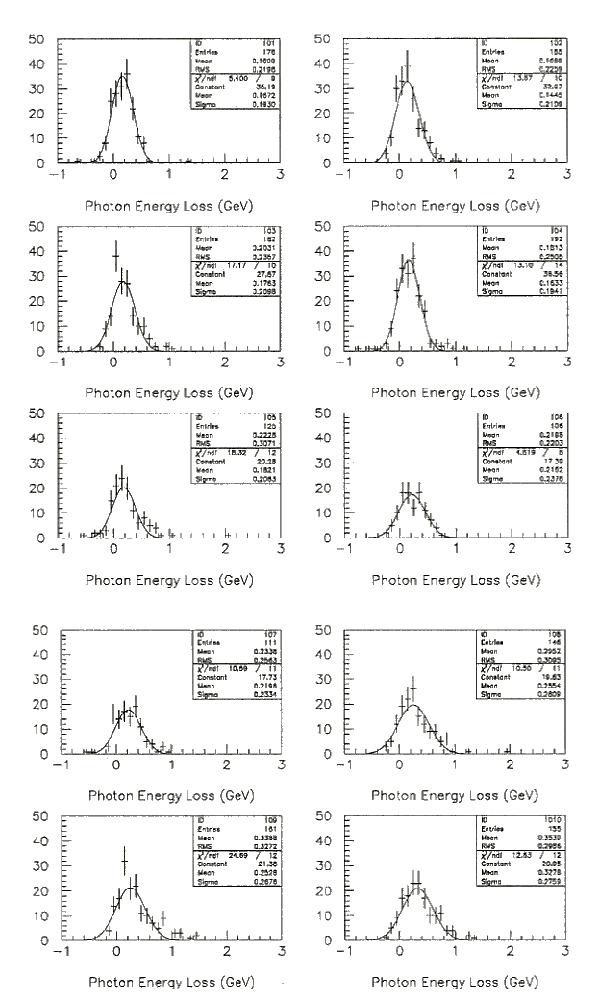
The average energy loss is taken as the mean of the Gaussian fit to the difference in the Monte Carlo energy and the deposited energy, DE_g, for a given bin in |cos(qg)|. Examples of the fitted curves for the energy loss of the single photon Monte Carlo is shown in Figure 7.1 for different bins in |cos(qg)|. The statistical mean and standard deviation of the data points in each bin is shown in the upper right hand corner of each of the fitted histograms. The resolution is then defined as the standard deviation of the fit, s_{DE_g}, for the given bin in |cos(qg)|.

Graphic: images/elossfit1a.gif

Figure 7.1: Energy Loss and Resolution of the Single Photon Monte Carlo Fits to energy loss of the single photons Monte Carlo from the process, e⁺e^-Ž n[`(n)]g, are used to determine the average energy loss, DE_g =E_g^corr-E_g^raw =E_g^four vec.-E_g^obs. and the resolution of the average energy loss, s_{DE_g}. The angular bins for each of the fits are the same as those plotted in Figure 7.2.

In Figure 7.2, the average energy loss and resolution points for the single photon Monte Carlo determined from the fits shown in Figure 7.1 are fit as a function of their expected dependence on angle. The form of the expected energy loss and resolution as a function of the angle is

DE_g(q)
=
a₀ + a₁ e^{-a₃ / sin q}

(7.2)
where

a₀
=
the first fit parameter determined to be 0.093840

a₁
=
the first fit parameter determined to be 0.001556

a₂
=
the first fit parameter determined to be -3.6930

The c² of the energy loss fit is 5.52/11, while the c² of the energy resolution is 6.77/11, both well below 1.0. The value of the energy loss used in the selection of the single photon events is the value determined from the empirical equation of the fitted energy loss points. The average energy loss for the single photon Monte Carlo events is 0.196 GeV and the average resolution is 0.219 GeV. This indicates that an E_g^corr cut at 1.75 GeV effectively accepts photons down to 1.5 GeV for a corresponding cut on E_g directly, while an E_g^corr cut at 1.75 GeV accepts photons down to 1.25 GeV. This agrees well with the Monte Carlo single photon events for e⁺e^-Ž n[`(n)]g which all have E_g of at least 1.47 GeV for a cut on E_g^corr at 1.75 GeVand all single photon events for e⁺e^-Ž n[`(n)]g which have an E_g of at least 1.28 GeV for a cut on E_g^corr at 1.5 GeV.

Graphic: images/eloss91b.gif

Figure 7.2: Single Photon Energy Loss and Resolution. The difference between the photon Monte Carlo energy and the energy deposited in the electromagnetic energy is due mainly to the energy loss in the coil. This energy loss given by Equation 7.1 is shown by the solid dots with statistical errors in (a) along with the energy resolution in (b) over photon polar angle with p < 5.0 GeV/c. The energy resolution is defined as the standard deviation of the Gaussian fit to the energy loss for the single photon events. The points have been fitted with a third degree polynomial resulting in the values shown.

7.2 The Single Electron Sample

A check of the consistency for the energy loss and resolution has been performed using the single electron events. These events are triggered by a superset of the same triggers for the single photon events shown in Section 4.3 and occur abundantly in the data. The single electron events were selected from the data corresponding to periods 20 to 33 collected during the 1991 run of OPAL using the same selection criteria as outlined in Section 6.1 with the following important changes:

_e^ą

The Monte Carlo programs used to generate the various physics processes have already been discussed in Section 5.3. The Monte Carlo generators used include: TEEGG [68] for the e⁺e^-Ž e⁺e^-g process and VERMAS [76] for the e⁺e^-Ž e⁺e^-e⁺e^-, the e⁺e^-Ž e⁺e^-m⁺m^-, and the e⁺e^-Ž e⁺e^-t⁺t^- processes. In all cases, the luminosity of the Monte Carlo events is more than five times that of the data. The events are selected with the same selection algorithm used for the single photon candidates. A summary of the production for the single electron studies is shown in Table 7.1 with the specific selection requirements of the Monte Carlo four vectors.

SINGLE ELECTRON MONTE CARLO PRODUCTION
Acceptance - At least one e^ą with E_e > 0.9 GeV and \|cos(q_e^ą)\| < 0.7,
other e^-± and photon with \|cos(qg)\| > 0.7.
RUN	PROCESS	GENER.	E_CM	EVTS.	L (pb^-1)
1301	e⁺e^- Ž e⁺e^-g	TEEGG	91.25	4572	3.10ą0.03
Acceptance - At least one e^ą with E_e > 2.0 GeV
and 0.75 < \|cos(q_e^ą)\| < 0.95, other e^ą and photon with \|cos(qg)\| > 0.95.
RUN	PROCESS	GENER.	E_CM	EVTS.	L (pb^-1)
1304	e⁺e^- Ž e⁺e^-g	TEEGG	91.25	3000	2.20ą0.04
Acceptance - At least one e^ą with E_e > 2.0 GeV and \|cos(q_e^ą)\| < 0.75,
and the other e^ą and photon with \|cos(qg)\| > 0.90.
RUN	PROCESS	GENER.	E_CM	EVTS.	L (pb^-1)
1305	e⁺e^- Ž e⁺e^-g	TEEGG	91.25	20000	10.18ą0.13
Acceptance - At least one e^ą with E_e > 2.0 GeV and \|cos(q_e^ą)\| < 0.75,
and no other particles with E_e > 0.9 GeV and \|cosq\| > 0.90,
and q_sep > 200 mrad.
RUN	PROCESS	GENER.	E_CM	EVTS.	L (pb^-1)
1710	e⁺e^- Ž e⁺e^-e⁺e^-	VERMAS	91.25	16929	10.01ą0.08
1712	e⁺e^- Ž e⁺e^-m⁺m^-	VERMAS	91.25	10091	10.01ą0.10
1714	e⁺e^- Ž e⁺e^-t⁺t^-	VERMAS	91.25	653	10.10ą0.39
Acceptance - At least one e^ą with E_e > 0.9 GeV and p_tot > 2.0 GeV
and 0.75 < \|cos(q_e^ą)\| < 0.92
RUN	PROCESS	GENER.	E_CM	EVTS.	L (pb^-1)
1711	e⁺e^- Ž e⁺e^-e⁺e^-	VERMAS	91.25	8143	10.01ą0.11
1713	e⁺e^- Ž e⁺e^-m⁺m^-	VERMAS	91.25	5617	10.01ą0.13
1715	e⁺e^- Ž e⁺e^-t⁺t^-	VERMAS	91.25	845	10.10ą0.34

Table 7.1: Monte Carlo Production for Single Photon Studies.

Using the above selection criteria, a sample of 14,946 single electron events have been selected in EB and a sample of 5441 single electron events in EE from the 1991 data. The agreement between the selected single electron events and Monte Carlo simulation from e⁺e^-Ž e⁺e^-g, e⁺e^-Ž e⁺e^-e⁺e^-, e⁺e^-Ž e⁺e^-m⁺m^-, and e⁺e^-Ž e⁺e^-t⁺t^- is excellent as shown in Figure 7.3 for the barrel and endcap regions. The corrections applied to the single electron selection include trigger inefficiencies (0.06ą0.02%), track inefficiencies (0.2ą0.2%), energy and dE/dx cut (-0.5ą0.5%), and 2^nd cluster veto (0.7ą0.7%). The total number of single electron Monte Carlo events selected in EB is 14,672.9, while the total number of single electron Monte Carlo events selected in EE is 5488.4.

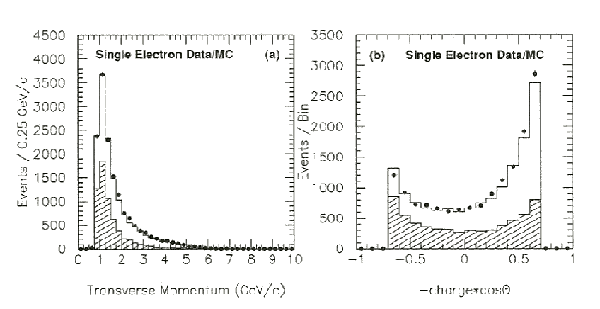
Graphic: images/e91eb.gif

Figure 7.3: Single Electron Spectra in the Barrel The transverse momentum spectrum (a) and the angular distribution (b) of the single electron events is shown. The combined data with statistical errors is shown by the solid dots, while the shaded histogram show the contribution from the reactions e⁺e^-Ž e⁺e^-e⁺e^-, e⁺e^-Ž e⁺e^-m⁺m^-, and e⁺e^-Ž e⁺e^-t⁺t^-, and the unshaded area shows the expectation from e⁺e^-Ž e⁺e^-g normalized to the integrated luminosity of 12.167ą0.083 pb^-1.

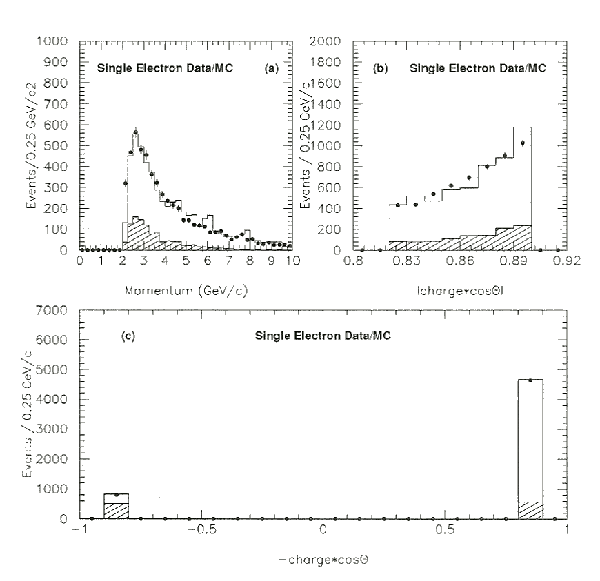
Graphic: images/e91ee.gif

Figure 7.4: Single Electron Spectra in the Endcap The transverse momentum spectrum (a) and the angular distribution (b) and (c) of the single electron events is shown. The combined data with statistical errors is shown by the solid dots, while the shaded histogram show the contribution from the reactions e⁺e^-Ž e⁺e^-e⁺e^-, e⁺e^-Ž e⁺e^-m⁺m^-, and e⁺e^-Ž e⁺e^-t⁺t^-, and the unshaded area shows the expectation from e⁺e^-Ž e⁺e^-g normalized to the integrated luminosity of 12.167ą0.083 pb^-1.

7.3 Single Electron Energy Loss and Resolution

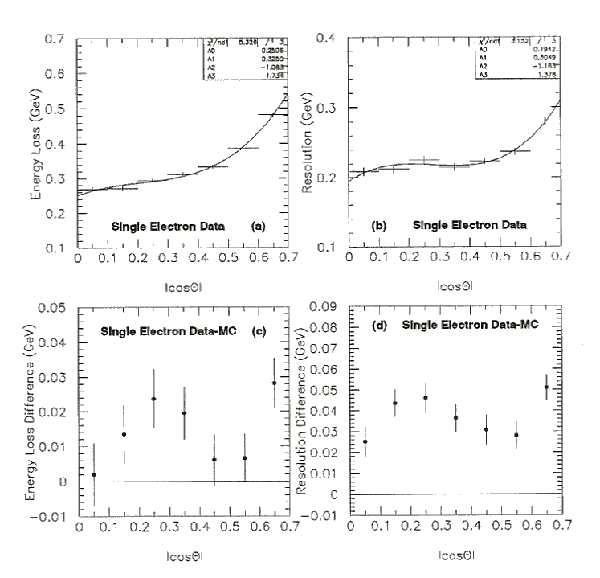
The energy loss for the single electrons is equivalently defined as the difference between the central detector momentum and the calorimeter energy of the electron. The single electron events are ideal since the momentum is well measured from the curvature of the track in the central detector and can be compared directly to the electromagnetic calorimeter shower. Figure 7.5(a) and (b) shows the energy loss and resolution of the single electron data set as a function of angle with p < 5.0 GeV/c. In Figure 7.5(c) and (d) is the difference in the energy loss and resolution between the data and Monte Carlo for the single electrons as a function of polar angle with p < 5.0 GeV/c. From the agreement between the calorimeter energy loss and resolution in the coil, the data seem to be well simulated.

Graphic: images/eeloss91.gif

Figure 7.5: Single Electron Energy Loss and Resolution The energy loss is defined as the difference in the electron momentum measured by the central detector and by the electron energy from the electromagnetic calorimeter. The energy loss is shown by the solid dots with statistical errors in (a) along with the energy resolution in (b) over photon polar angle with p < 5.0 GeV/c. The difference in the energy loss between the single electron data and Monte Carlo is shown in (c) along with the corresponding difference for the resolution shown in (d).

For the single electron events considered in EB, the average energy loss of the electrons due to the coil is 0.360 GeV with an average discrepancy of 0.010 GeV more than the energy loss of the Monte Carlo. The energy resolution is typically 0.250 GeV which is about 0.025 GeV more than that of the Monte Carlo. For the single electron events considered in EE, the average energy loss of the electrons due to the coil is 0.740 GeV with an average discrepancy of 0.123 GeV more than the energy loss of the Monte Carlo. The energy resolution is typically 0.315 GeV which is about 0.114 GeV more than that of the Monte Carlo. Specifically for single electron energies of 1.30 GeV in the barrel, the data and Monte Carlo simulation agree to within 0.025 GeV for the energy loss and 0.028 GeV for the resolution of the energy loss.

With the simulation of the single photon events in the barrel similar to the simulation of the single electron events, the uncertainty in the energy scale for photons with E_g^corrnear 1.50 GeV would correspond to the uncertainty in the energy scale for the single electron events with E_gnear 1.30 GeV. The corresponding uncertainty in the energy scale for the single photon events is 0.025 GeV with a resolution of 0.028 GeV. The systematic error associated with this uncertainty is determined by varying the cut on E_g^corr by this amount, selecting single photon candidates and determining the number of neutrinos based upon the selected events (refer to Chapter 10). From such considerations, the systematic error introduced by the energy scale is determined to be 3.12% as shown in Table 10.2.

Chapter 7 Single Photon Energy Loss and Resolution

7.1 Single Photon Energy Loss and Resolution

7.2 The Single Electron Sample

7.3 Single Electron Energy Loss and Resolution

Chapter 7
Single Photon Energy Loss and Resolution