Chapter 10
Results and Conclusions
From periods 20 through 33 of the 1991 run, 201 events with corrected energy,
Egcorr, greater than 1.5 GeV are observed.
The events have been selected using the selection criteria given in
Section 6.1.
Historically, the single photons have been divided into two samples according
to the corrected energy of the accepted photon in order to understand the
backgrounds and efficiencies.
The first sample consists of 46 observed single photon events with
1.5 GeV < Egcorr < 1.75 GeV, while the second sample consists of 155 single
photon with Egcorr ³ 1.75 GeV.
The two samples are then combined to improve the statistical error for the
measurements presented in this thesis.
Each single photon event has been visually scanned as a check for consistency
of the selection and events.
This chapter discusses the results of the analysis of the single photon signal.
10.1 Two Single Photon Samples
The single photon candidates with 1.5 GeV < Egcorr < 1.75 GeV are compared to
the Monte Carlo expectations for the total single photon signal as shown in
Figure 10.1.
The spectra compare the total Monte Carlo from single photon process e+e-® n[`(n)]g
and the backgrounds as discussed above corrected for the efficiencies
for the single photon candidates.
For the first sample, 46 single photon events selected with an average
efficiency of 59.4±1.4% and an expected background of 18.39±3.43 events.
A total of 47.77±1.42 single photon events are expected from Monte
Carlo with 29.38±0.88 originating from the e+e-® n[`(n)]g signal.
From the degree of agreement between the data and the Monte Carlo, it is seen
that the backgrounds and efficiencies are well understood for this sample.
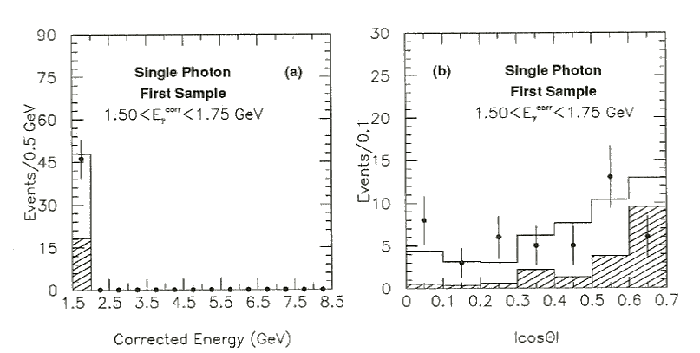
Figure 10.1: Single Photon Spectra for the First Sample.
The corrected photon energies for all single photon events in the first
sample with 1.5 GeV < Egcorr < 1.75 GeV are shown in (a) along with the
angular spectrum for photons in (b).
The single photons from the Monte Carlo are shown corrected for trigger, veto,
and selection efficiencies, for the signal process e+e-® n[`(n)]g by the unshaded
histograms and the backgrounds by shaded histograms.
The histograms are similar to the set of histograms shown later for the
second sample.
The single photon spectra for the selected events with
Egcorr ³ 1.75 GeV are shown in Figure 10.2 for three different
center-of-mass regions: Ös < MZ0, Ös=MZ0, and Ös > MZ0.
The spectra show the single photon data compared to the Monte Carlo background
and signal, e+e-® n[`(n)]g for Nn=3, normalized to the total recorded luminosity.
The second sample consists of 155 single photon events selected with an
average efficiency of 64.5±1.2% with an expected background of 12.31±2.24 events.
A total of 149.20±4.45 single photon events are expected from Monte
Carlo with 136.90±4.08 originating from the e+e-® n[`(n)]g signal.
The Monte Carlo is corrected for trigger, veto, and selection efficiencies and,
in general, is in very good agreement with the data.
Figure 10.2: Single Photon Spectra for the Second Sample.
The corrected energies for all selected single photon events are shown
for Ös < MZ0 in (a), for Ös = MZ0 in (c), and
for Ös > MZ0 in (e).
The corresponding angular spectra for all selected single photon events are
shown for Ös < MZ0 in (b), for Ös = MZ0 in (d), and
for Ös > MZ0 in (f).
The single photon events from the data are shown in solid dots with
statistical errors.
The single photon events from the Monte Carlo are corrected for trigger and
selection efficiencies and shown by the unshaded histograms for the process
e+e-® n[`(n)]g, and the shaded histograms for the backgrounds.
From level of agreement between the data and the Monte Carlo of the single
photon spectra for the first and the second samples, the two samples are
combined to determine the total cross-section at each center-of-mass energy
point.
The total cross-section at each center-of-mass energy point for the data
is listed in Table 10.1 and shown in Figure 10.3 along
with the expected total cross-sections for Nn=2, Nn=3 and Nn=4.
The cross-sections are determined from the total integrated luminosity and
the number of single photon events corrected for trigger, veto, and selection
efficiencies with background subtracted.
These values are compared to the expected total cross-sections for Nn=2
and Nn=4 with an analytical program [27].
The analytical program determines cross-sections from the ``reduced''
cross-section for the e+e-® n[`(n)]g process given by Equation 2.15.
The program uses an improved Born approximation and the structure function
method to include higher order electromagnetic radiative corrections through
an s-dependent GZ0.
In applying the program, the GZ0inv is specified by
Ginv=NnGn and the number of neutrino families, Nn, is
allowed to vary.
The input parameters used for the program are taken from the most recent
measured values of OPAL and include
the Z0 mass, MZ0=91.181±0.007±0.006 GeV [89],
the Z0 width, GZ0=2.483±0.011±0.004 GeV [89],
and sin2[`(q)]w=0.232±0.003 [18].
| Ös | sMC (pb) | sMC (pb)
| sMC (pb) | sData (pb) |
| (GeV) | (Nn=2)
| (Nn=3) | (Nn=4)
| Egcorr > 1.50 GeV |
|
|
| 88.45 | 3.15 | 4.72 | 6.30 | 2.04±3.02±0.15 |
| 89.45 | 4.52 | 6.78 | 9.04 | 11.21±5.61±0.81 |
| 90.20 | 6.32 | 9.49 | 12.65 | 21.91±7.18±1.53 |
| 91.20 | 10.75 | 16.12 | 21.49 | 15.25±1.92±0.93 |
| 91.95 | 17.62 | 26.43 | 35.24 | 34.02±8.37±2.37 |
| 92.95 | 32.24 | 48.36 | 64.47 | 45.37±9.64±3.15 |
| 93.70 | 39.77 | 59.66 | 79.54 | 61.18±11.17±4.27 |
Table 10.1: Total Cross-Sections for Both Single Photon Samples (1991).
From the number of single photon events with Egcorr ³ 1.50 GeV
in the angular range |cos(qg)| £ 0.7, the total cross-section at each
center-of-mass energy point for the data is determined from the total
integrated luminosity and the number of single photon events corrected
for trigger, veto, and selection efficiencies with background subtracted.
These values are compared to the expected total cross-sections for Nn=2
and Nn=4 determined with an analytical program which evaluates the
``reduced'' cross-section for the e+e-® n[`(n)]g process given by
Equation 2.15.
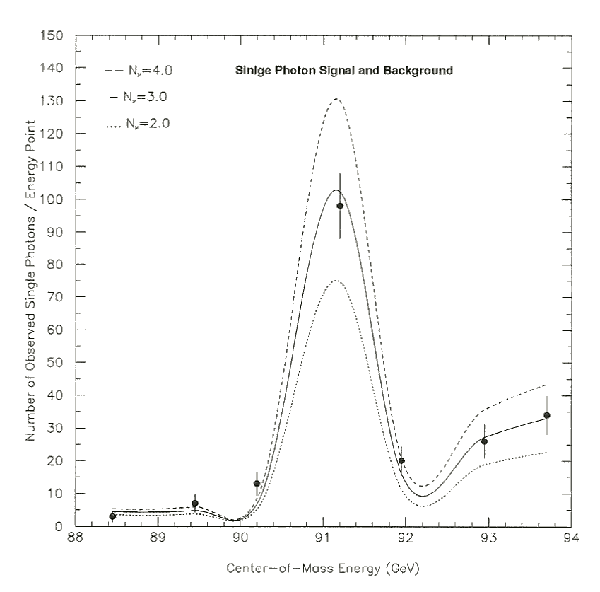
Figure 10.3: The Single Photon Total Cross-Sections.
The corrected cross-sections (pb) at each center-of-mass energy point
for the single photon candidates with Egcorr ³ 1.5 GeV in the angular
range |cos(qg)| £ 0.7 from the process e+e-® n[`(n)]g.
The data points are shown in solid dots with statistical errors.
The number of events expected for Nn = 2, 3, and 4 is shown by the dotted,
solid, and dashed lines, respectively.
The analytical program described above has also been used to calculate the
number of observed events expected at each center-of-mass energy point.
The number of observed events from the data are fit to the number of predicted
events as a function of Nn using the method of maximum-likelihood in the
limit of Gaussian event distributions.
The analytical program and fitting procedure have been tested for consistency
with the single photon Monte Carlo events yielding agreement to within 2%
of the number of neutrino families used to generate the Monte Carlo events.
The result for the fit of the observed single photon events from the 1991 data
set is 3.01±0.25 (statistical error) with a c2 of 5.37/6.
Figure 10.4 shows the number of single photon events observed at
each center-of-mass point with the corresponding predictions for Nn = 2, 3,
and 4.
Figure 10.4: Fit to the Number of Observed Single Photon Events.
The number of observed events from the 1991 data set is fit to the expected
number at each center-of-mass energy point using the method of
maximum-likelihood in the limit of Gaussian event distributions.
The data points are shown in solid dots with statistical errors.
The number of events expected for Nn = 2, 3, and 4 is shown by the dotted,
solid, and dashed lines, respectively.
10.2 Systematic Errors
The systematic error for the single photon measurement originates from
essentially three sources: first, the efficiencies, second, the energy loss
calculation, and last the background and luminosity measurement.
Each of these contributions has been determined from the 1991 data set for this
analysis and is summarized in Table 10.2.
The total systematic error for the 1991 data set is 4.9% to be compared with
the 1990 data set of 5.6%.
Most of the reductions in the systematic error over the previous OPAL result
can be traced to increased statistics for dedicated selection studies and
perhaps improvements in the OPAL simulation code.
The largest contribution to the systematic error from the previous published
OPAL result originated from the selection efficiency.
For the analysis presented here, the largest contribution to the systematic
error originates from the energy loss.
The reason for this large difference is directly related to the way in which
the total cross-sections for the data set are determined.
This analysis incorporates the average energy loss due to the material in front
of the electromagnetic calorimeter, especially the coil, directly in the
selection of the single photon events used to determine the total
cross-sections at each energy point.
The previous analysis incorporates this energy loss by normalizing the number
of accepted events to the number of Monte Carlo events otherwise accepted at
the four-vector level.
The quoted uncertainty in the determination of such coefficients is 2% which,
added in quadrature to the systematic error in the acceptance from the energy
scale, 2.1%, gives 2.9% reflecting the conservative nature of the systematic
errors quoted in this analysis.
The systematic errors for the combined 1990 and 1991 data sets are determined
by weighting the different systematic errors from each data set according to
the number of events,
|
|
| | |
|
å
i
|
|
é
ê
ë
|
wi |
æ
ç
è
|
dNni
|
ö
÷
ø
|
ù
ú
û
|
|
|
| | |
|
|
| (10.1) |
where ni is the number of single photon events observed.
The combined systematic error is shown in Table 10.2 along with the
separate contributions to the systematic errors for the previous analysis
from the 1990 data set and this analysis with the 1991 data set.
| SOURCE | 1990 | 1991 | COMBINED |
|
|
| Trigger-Eff. | 0.1% | 0.2% | 0.2% |
| Selection.-Eff. | 4.0% | 3.0% | 3.4% |
| Veto-Eff. | 0.1% | 0.1% | 0.1% |
| Energy Loss | 2.1% | 3.1% | 2.8% |
| Backgrounds | 2.7% | 2.0% | 2.3% |
| Luminosity | 1.6% | 0.7% | 1.1% |
| Misc. | 1.0% | 1.0% | 1.0% |
|
|
| TOTAL | 5.6% | 4.9% | 5.1% |
Table 10.2: Systematic Errors of the Single Photon Measurement.
The systematic error originates primarily from the efficiency,
the energy loss, and the background and luminosity measurement.
Column 1 gives the contributions to the previous measurement from the 1990
data set, Column 2 gives the contributions to the present measurement with the
1991 data set, and Column 3 gives the contributions to the combined
event-weighted measurement from the 1990 and 1991 data sets.
10.3 The 1991 Measurement of Nn and GZ0inv
Including the systematic errors in the determination of the number of light
neutrinos, the measurement from the 1991 data set yields Nn=3.01±0.25±0.15.
The invisible width of the Z0 can be determined from the number of light
neutrinos assuming that the W± contribution is that predicted by the Standard
Model and that no other visible particles couple to the Z0.
The value of the invisible width determined in this way from the measurement
of the number of light neutrinos for the 1991 data set is 502±42±25 MeV.
By combining the two samples the statistical errors is reduced by almost 8%
for these measurements.
10.4 The Combined Measurement of Nn and GZ0inv
Using the 1990 data set and the 1991 data set together, a combined limit on
the number of neutrino families, Nn, and the Z0 invisible width, GZ0inv,
can be obtained.
The combined limit is obtained by using a standard method for averaging
uncorrelated data with highly correlated systematic errors [4].
The combined measurement for the number of light neutrinos, Nn, is obtained
from the weighted average with statistical errors according to
where Nn and dNni are the measured value and the statistical
error.
The value of c2 is calculated from
and compared with the expectation value N - 1 for a Gaussian distribution.
The combined measurement is determined to be 3.01±0.22 (statistical error).
The value of c2 is determined to be 0.06, well below 1.0 for a Gaussian
distribution.
Including the systematic errors in the determination of the number of light
neutrinos, the combined measurement from the 1990 and 1991 data sets yields
Nn=3.01±0.22±0.16 MeV.
The value of the invisible width determined from the combined measurement of
the number of light neutrinos is 502±35±27 MeV.
The total cross-sections for the 1990 and 1991 data sets together was fitted
and yielded comparable results.
10.5 Conclusions
With the 1991 data set collected by OPAL, an improved measurement of the number
of light neutrinos is made by measuring the single photon cross-section.
In a data sample of 13.076±0.089 pb-1, 201 events with corrected energy,
Egcorr, greater than 1.5 GeVare selected.
These 201 events are used to determine the number of light neutrinos,
Nn = 3.01±0.25±0.15.
With the 1990 data set from the previous analysis [21], a
combined measurement of the number of light neutrinos yields Nn=3.01±0.22±0.16.
This result rules out Nn=2 and Nn=4 at the 99% confidence level.
In the Standard Model coupling of the Z0 to the neutrinos, this corresponds
to the invisible width, GZ0inv=502±35±27 MeV.
The results from the previous analysis of the 1990 data set, the present
analysis of the 1991 data set, and the combined analysis of the 1990 and 1991
data sets are shown in Table 10.3.
The present measurements are important since they are significant improvements
over the previous OPAL results and compatible with the best measurements to
date shown in Table 10.4.
| DATA SET | GZ0inv (MeV) | Nn |
|
|
| 1990 | 500±67±33 | 3.0±0.4±0.2 |
| 1991 | 502±42±25 | 3.01±0.25±0.15 |
|
|
| COMBINED | 502±35±27 | 3.01±0.22±0.16 |
Table 10.3: Measurements of Nn and GZ0inv Using the Single Photon Counting Method.
The results of the measurements for GZ0inv and Nn using the single photon
counting method from the analysis of the 1990 data set, this analysis of the
1991 data set, and the combined 1990 and 1991 data sets are shown.
The first error shown is the statistical error, while the second error is the
systematic error.
| EXPERIMENT | GZ0inv | Nnfit |
|
|
| Cosmology [11] | < 550 (90% C.L)
| < 3.3 (90% CL) |
| < 600 (95% CL) | < 3.6 (95% CL) |
|
|
| ASP, CELLO, MAC [12] | < 650 (90% C.L)
| < 3.9 (90% CL) |
| < 800 (95% CL) | < 4.8 (95% CL) |
|
|
| L3 [20] | 524±40±20 | 3.14±0.24±0.12 |
| OPAL [21] | 500±67±33 | 3.0±0.4±0.2 |
|
|
| COMBINED | 502±35±27 | 3.01±0.22±0.16 |
|
|
| LEPave [18]
| 497±9 | 2.99±0.05 |
Table 10.4: Measurements of Nn and GZ0inv.
The best measurements for GZ0inv and Nn are summarized for the different
sources of measurement.
Historically, the best limits were derived from cosmological considerations
of primordial matter.
The higher rate of Z0 production at the LEP collider allowed for superior
results over the previous early collider experiments of ASP, CELLO, and MAC.
Presently, the best measurements using the method of invisible width or
the single photon counting method come from the LEP experiments.
The first error shown is the statistical error, while the second error is the
systematic error.
Finally, the method of single photon counting can also be used to place limits
on new particles that interact only weakly with matter and are not directly
observable.
When accompanied by the radiation of a single photon, such new particles with
the signature
e+e- ® g+ wips (weakly interacting particles)
resemble the experimental signature of a single photon in the final state
from the process e+e-® n[`(n)]g.
Minimal theories of supersymmetry (SUSY) [92] predict that such new
particles as the photino, [(g)\tilde], and scalar neutrinos,
[(n)\tilde], are produced in pairs by the exchange of a scalar electron
or currents.
As a consequence these interactions,
e+e- ® [(g)\tilde] [(g)\tilde]g and
e+e- ® [(n)\tilde] [([`(n)])\tilde] g, result in
the same signature as the process e+e-® n[`(n)]g in the detector.
However, since other authors have already placed limits in excess of 51 GeV
[93], the single photon signature for the pair production
of such particles at LEP is insignificant until Ös » 102 GeV,
namely at LEP200.