Appendix A
Gauge Theories

Perhaps the most important reason for our present understanding of the fundamental interactions of elementary particles is our understanding of the underlying symmetries guiding such interactions. Such symmetries manifest themselves in both locally and globally conserved physical quantities, like electric charge, which eventually lead to conservation laws. The important class of theories describing these symmetries are known as gauge symmetry theories. This chapter presents an short overview of gauge symmetry theories and focuses on the most important aspects of such theories.

The Structure of Gauge Symmetry Theories

Notice that < O > is invariant under a global phase transformation of the form y(x) ® e^iea(x)y(x) , where a is any scalar. On the other hand, the gradient of the wave function, ¶_my(x) ® e^iea(x)[ ¶_my(x)+iey(x)¶_ma(x) ] yields y^*(x)¶_my(x) and is not invariant. To satisfy gauge invariance, ¶_m is replaced by the covariant derivative D_m = ¶_m - ieA_m and a local gauge transformation on the field A_m to A_m(x) + ¶_m a(x)/e. Under the simultaneous phase transformation on ¶_my(x) and the gauge transformation on A_m(x), D_my(x) = e^iea(x)D_my(x) and y^*(x)D_my(x) is again invariant.

Furthermore, the mathematical relation of the wavefunction, y(x), and the interactions described by fields, A_m, defines the Lagrangian, L_y(x), of the theory which satisfies the Euler-Lagrange ``minimization equation'' [90],

¶ ¶xm æ è  ¶L ¶(¶y/¶xm) ö ø -  ¶L ¶y = 0

(A.1)

The resulting equations describe the motion and conserved quantities associated with the theory. The gauge invariance leads to the conserved observables of the theory, < O > , while the Euler-Lagrange type ``minimization equation'' leads to the conservation laws associated with the field A_m.

As an example of a local gauge invariance, consider the spatial transformation of the quantum mechanical wavefunction a spin 1/2 fermion of the form y(x)® e^ia(x)y(x). The wavefunction is associated with a vector field, A_m, which is used to parametrize the Lagrangian function, L_y(x). For an half spin fermion interacting via the electromagnetic interaction, the Lagrangian takes on the form,

Ly(x) = - y(x)   (igm¶m-m)y(x) + e - y(x)   gmy(x) Am-  1 4 FmnFmn

(A.2)

Here [`(y(x))](ig<sup>m</sup>¶<sub>m</sub>-m)y(x) is the kinetic and mass term of the half spin fermion (electron), e[`(y(x))]g^my(x) A_m is the coupling of the photon field, A_m, and the electron current j_m=e[`(y(x))]g^my(x), and F_mn=¶_mA_n-¶_nA_m is the kinetic term of the photon field. The gauge invariance of the electromagnetic interaction leads to charge conservation and the masslessness of the photon associated with electromagnetic field A_m, while the solution of the Euler-Lagrange ``minimization equation'' for the quantum electrodynamics (QED) Lagrangian leads to the compact form of Maxwell's equations, ¶_mF^mn=jⁿ.

While gauge invariance leads to conserved quantities and the solution of the Euler-Lagrange equation leads to the equations of motion for the theory, such observables as the relative rate in time for a process is predicted from the invariant transition amplitude. The invariant transition amplitude is calculated with the assistance of a system of diagrams and rules derived ultimately from the Lagrangian describing the theory. The diagrams, called Feynman diagrams, graphically illustrate the interaction of particles with the fields in the theory. Each element of the Feynman diagram, such as a line, a vertex, etc., carries a specific mathematical significance in the calculation of the invariant amplitude according to the Feynman rules derived from the Lagrangian of the theory.

Feynmann Rules

The interaction of the particles derived from the QED Lagrangian, L, is shown in the Feynman diagram. The most important interaction between fermions is the g-l Interaction with the vertex representing the photon-fermion interaction of the form

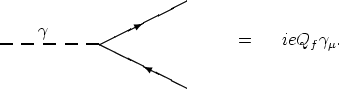
with the identification of A_m as the photon field.

The Invariant Amplitude

In the extreme relativistic limit, the cross-section for the process e⁺e^-® e⁺e^-m⁺m^-  reproduces the familiar (1+cos²q) dependence as follows:

ds dW cm  =  a2 4 s2 (1+cos2q)

(A.5)

Integrating over solid angle, dW, gives the familiar QED result,

stot =  4pa2 3 s2

(A.6)

which has been tested tested through scattering experiments. Such observables calculated using QED like the hyperfine structure have been calculated and tested to an extremely high degree of accuracy (1 part in 2,899,131 [91]).