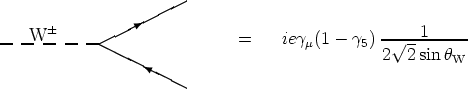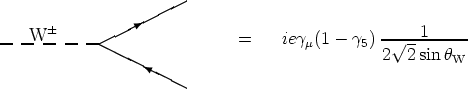The Standard Model (SM) is composed of two gauge symmetry theories which
collectively describe the electroweak and strong interactions of elementary
particle physics.
The Glashow-Salam-Weinberg Model (GSW) [10] describes electroweak
interactions through the SU(2)LÄU(1)Y gauge symmetry theory,
while Quantum Chromodynamics (QCD) [94] describes the strong
interactions through the SU(3)C gauge symmetry theory.
The ``minimal'' Standard Model consists of the spontaneously broken gauge group
SU(3)C ÄSU(2)L ÄU(1)Y with three generations of
quarks and leptons and one physical Higgs particle.
Assuming massless neutrinos (or equivalently that there are not right-handed
neutrinos) and no strong CP-violation,
The SM requires eighteen external parameters as follows [95]:
(1) Three gauge couplings; a, as, and GF.
(2) Two parameters representing the Higgs sector; < f > and
mf.
(3) Nine masses spread over five orders of magnitude for the six
quarks and three charged leptons.
(4) Three Cabibbo angles and one phase factor for the mixing of
the quark mass eigenstates.
The SM is, to-date, the most complete and widely accepted gauge theory
describing electromagnetic, weak, and strong interactions.
This appendix presents an overview of the Standard Model with an emphasis on
the electroweak component (GSW) of the theory since this specifically applies
to the analysis presented in this thesis.
The Glashow-Salam-Weinberg Model (GSW)
In 1967, S. Glashow, S. Weinberg, and A. Salam proposed a gauge theory based
on the group of transformations generated by the weak isospin and hypercharge
generators associated with the group product of the
SU(2)L ÄU(1)Y [10].
The SU(2)L group provides a triplet of gauge fields,
Wm = Wm1, Wm2, Wm3, coupling to
weak isospin, T, and describes the weak interactions between left-handed
fermions and right-handed anti-fermions.
The U(1)Y group results in a singlet field, Bm, and couples to
weak hypercharge, Y.
As a result of the gauge symmetry, each family of fermions can be classified
into left-handed doublets of weak isospin or right-handed singlets,
|
cLl = |
æ
ç
è
|
|
ö
÷
ø
|
L
|
and fRl = l where l = e, m, t |
|
|
cLq = |
æ
ç
è
|
|
ö
÷
ø
|
L
|
and fRq = q , q¢ where q = u, c, t |
| (B.1) |
The symmetry group SU(2)L is non-abelian due to the fact that its
generator, Ti=[ 1/2]ti, satisfies the non-Abelian algebra
[Ti,Tj]=i fijkTk.
The non-Abelian nature of the SU(2)L symmetry group leads the
self-interaction of the gauge bosons associated with the group.
The left-handed doublets, cLl and cLq, transform under
the actions of the generators of the SU(2)L symmetry group, Ti, while
the right-handed singlets, fRl and fRq, transform only
under the action of the hypercharge generator according to
where Q is the electromagnetic charge, T3 is the third component of
isospin, and Y is the weak hypercharge.
The Electroweak Interaction Energy
The electroweak interaction energy is obtained by requiring the following
i) The invariance of the theory under the local gauge
transformation:
ii) The inclusion of covariance derivatives, Dm, of the
form
iii) The inclusion of kinetic terms for the vector bosons of the
form
iv) The inclusion of a mechanism to generate fermion masses as
well as the mass of the observed W± and Z0 bosons, while keeping the photon
massless.
The ``Higgs Mechanism'' spontaneously breaks symmetry by introducing an SU(2)
doublet of complex scalar fields with hypercharge Y = 1 of the form:
|
f = |
æ
ç
ç
ç
è
|
|
ö
÷
÷
÷
ø
|
= |
æ
Ö
|
|
|
æ
ç
ç
ç
è
|
|
ö
÷
÷
÷
ø
|
= |
æ
Ö
|
|
|
æ
ç
ç
ç
è
|
|
ö
÷
÷
÷
ø
|
|
|
where the potential and kinetic energy contributions to the Lagrangian are of
the form:
|
|
| | |
| | |
(¶mf+ig |
1
2
|
t·Wmf)f(¶mf+ig |
1
2
|
t·Wmf) |
|
|
|
|
The electroweak interaction energy is usually represented by the Lagrangian
energy density, L, of fermions with the fields W, Bm
as follows [91]
|
|
| | |
- |
1
4
|
Wmn·Wmn- |
1
4
|
BmnBmn
|
|
|
|
| (B.2) |
|
|
| | |
|
-
c
|
L
|
gm |
æ
è
|
i ¶m-g |
1
2
|
t ·Wm-g¢ |
Y
2
|
Bm |
ö
ø
|
cL |
|
|
|
| (B.3) |
|
|
| | |
|
-
y
|
R
|
gm |
æ
è
|
i ¶m-g¢ |
Y
2
|
Bm |
ö
ø
|
yR |
|
|
|
| (B.4) |
|
|
| | |
|
ê
ê
|
æ
è
|
i ¶m-g |
1
2
|
t·Wm-g¢ |
Y
2
|
Bm |
ö
ø
|
f |
ê
ê
|
2
|
-V(f) |
|
|
|
| (B.5) |
|
|
| | |
(G1i |
-
c
|
L
|
fyR+G2i |
-
c
|
L
|
fcyR+ Hermite Complex Conjugate ) |
|
|
|
| (B.6) |
In general, the fundamental vector bosons are associated with the massless
vector triplet in the expression,
Wm = Wm(1), Wm(2), Wm(3) from SU(2)L
and a massless singlet Bm from U(1)Y.
As a result of spontaneous symmetry breaking, three bosons (denoted
Wm+,Wm-, and Zm) acquire mass, while one (Am, the photon) remains
massless.
The electroweak current incorporates the SU(2)L and U(1)Y currents
Q = T3 + [(Y)/2].
Each of the terms in the Lagrangian energy density is the result of a specific
energy density associated with the electroweak theory.
* Equation B.2 represents the kinematic energies and
interactions of the intermediate vector bosons, W±, Z0, and g.
* Equation B.3 represents the kinematic energies and
their interactions of the intermediate vector bosons with the right-handed
leptons and quarks.
* Equation B.4 represents the kinematic energies and
their interactions of the intermediate vector bosons with the left-handed
leptons and quarks.
* Equation B.5 gives the masses and couplings of the
intermediate vector bosons and the Higgs particle.
* Equation B.6 gives the masses of leptons and quarks
and their coupling to the Higgs particle where cL, yR are the
fermion weak isospin doublets and singlets.
Electroweak Mass Terms
The Lagrangian energy density of the electroweak theory gives rise to
the masses of the bosons and fermions in the theory.
These masses are derived by considering each term of the particle field
interactions from the term given by Equation B.6.
For example, in the case of the electron, the mass is obtained from the term
Gev [`(e)] e /Ö2 which yields the mass of me=Gev/Ö2
depending on the arbitrary parameter Ge.
Hence, the Higgs mechanism makes no predictions for fermion masses since each
mass term has an arbitrary constant Ge.
The mass term led by the gauge invariant Higgs-field interaction in the
Lagrangian energy density of the electroweak theory gives rise to the masses
of the three bosons (denoted Wm+, Wm-, and Zm), while rendering the
the photon, Am, massless.
|
|
|
|
ê
ê
|
æ
è
|
-g |
t
2
|
·Wm- |
i
2
|
g¢Bm
|
ö
ø
|
f |
ê
ê
|
2
|
|
| | |
|
1
8
|
|
ê
ê
ê
|
æ
ç
è
|
|
ö
÷
ø
|
|
æ
ç
è
|
|
|
ö
÷
ø
|
ê
ê
ê
|
2
|
|
|
| | |
|
1
2
|
|
æ
è
|
1
2
|
v g |
ö
ø
|
2
|
( Wm(1) 2 + Wm(2) 2 ) + |
v2
8
|
(Wm(3),Bm) |
æ
ç
è
|
|
|
ö
÷
ø
|
|
æ
ç
è
|
|
|
ö
÷
ø
|
|
|
|
|
| (B.7) |
The physical content becomes transparent by performing the transformation from
the fields W and Bm to the ``physical'' fields:
In these fields the mass terms are the diagonals of the matrix form of
Equation B.9 and are given by
|
|
| | |
|
1
2
|
vg and MZ
= |
1
2
|
v |
Ö
|
g2+g¢2
|
|
|
|
|
| (B.11) |
if the mixing angle in Equation B.8 B.9
B.10 is chosen as
Identifying Am with the photon field which couples via
the electric charge e=Ö{4pa} to the electron,
e can be expressed in terms of the gauge couplings
in the following way
|
|
| | |
|
gg¢
|
and |
g
g¢
|
= |
sinqW
cosqW
|
|
|
|
|
| (B.13) |
Identifying the coupling constant g with the Fermi constant GF from the
low energy regime
fixes the vacuum expectation parameter v=(GFÖ2)-1/2 @ 246 GeV.
The weak mixing angle, qW, relates the weak isospin coupling constant
g and the hypercharge coupling constant g¢ through the relation
g¢=g tanqW.
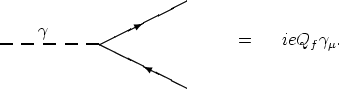
Electroweak Feynman Rules
The intrinsic rules for interactions of the elementary particles in a given
theory (Feynman Rules) are derived from the Lagrangian energy density of the
given theory.
For the important class of charged and neutral current processes between
fermions in the framework of electroweak theory, the coupling constants for the
vector and axial vector currents can be expressed in terms of the parameters
e, MW, MZ as follows:
where af and vf are the axial and axial vector coupling constants, Qf
is the electric charge of the fermion, f, gm and g5 are
the gamma matrices which are given by,
|
|
| | |
|
| | |
g1 g2 g3 g4 = |
é
ê
ê
ê
ê
ê
ë
|
|
|
ù
ú
ú
ú
ú
ú
û
|
|
|
|
|
| (B.15) |
The neutral current coupling constants are given by
|
|
| | |
|
I3f - 2Qfsin2qW
2sinqWcosqW
|
|
|
|
|
| (B.16) |
where I3f denotes the third isospin component of the fermion f.
The Z0 Coupling to Fermion Pairs
The differential cross-section for the coupling of the Z0 to fermions is
obtained for the electroweak theory with the aid of the Feynman Rules derived
from the Lagrangian energy density.
The invariant amplitude for the process e+e-® f[`(f)] can be expressed as
|
|
| | |
-i |
æ
Ö
|
|
ela |
-
u
|
ga(vf+afg5)v |
|
|
|
| (B.18) |
where e is the polarization vector of the Z0, [`(u)] and v are
the spinor for the fermion, f, and the Z propagator normalized to the
photon propagator is taken as,
The partial width for the decay process Z0® f[`(f)] is the
square of the invariant amplitude and can be expressed in the lowest order as
|
|
| | |
| | |
|
å
f
|
NfC |
a
3
|
MZ |
Ö
|
1-4mf
|
[ vf2 (1+2mf) + af2 (1-4mf) ] |
|
|
|
| (B.19) |
where NCf = 1, 3 for f = lepton, quark, mf=mf2/s,
a = (Ö2GFMW2sin2qW)p, and the Z-fermion
vector and axial couplings are given by Equations B.18.
The lowest order partial widths for various fermions are listed in
Table B.1 [24].
| f | If3 | Qf | G0(Z0 ® f[`(f)]) |
|
|
| n | 1/2 | 0 | 170 MeV |
| e | -1/2 | -1 | 85 MeV |
| u | 1/2 | 2/3 | 305 MeV |
| d | -1/2 | -1/3 | 392 MeV |
Table B.1: Lowest Order Partial Widths for Z0 Decay.
The lowest order partial widths for the Z0 decay are determined for each
of the different fermion channels according to the Standard Model.
The differential cross-section
s( e+e-® Z0® f[`(f)]) can be written in the form
|
|
| | |
| | |
|
é
ë
|
G1(s) (1+cos2q) + G3(s) 2cosq |
Ö
|
1-4mf
|
+ G2(s) sin2 q4mf |
ù
û
|
|
|
|
|
| (B.20) |
where
|
|
| | |
Qe2 Qf2 + 2Qe Qf ve vf Re( c0(s) ) + (ve2+ae2)(vf2+af2-4mfaf2) | c0(s) | 2 |
|
| | |
Qe2 Qf2 + 2Qe Qf ve vf Re( c0(s) ) + (ve2+ae2)vf2 | c0(s) | 2 |
|
| | |
2Qe Qf ae af Re( c0(s) ) +4ve ae vf af | c0(s) | 2 |
|
|
|
|
In the region where s » MZ02, this expression can be
reduced in terms of the of the partial widths GZ0e+e- and
GZ0f[`(f)] as follows
|
|
| | |
|
12 pGZ0e+e-GZ0f[`(f)]
(s - MZ02)2 + MZ02 GZ0tot2
|
|
|
|
|
| (B.21) |
which is a special case of the first order Breit-Wigner resonance formula.
Quantum Chromodynamics (QCD)
The second of the two gauge symmetry theories which form the Standard Model is
SU(3)C describing the strong interactions between quarks.
The SU(3)C group provides an octet of gauge fields, blm, coupling
to the ll generators and describing the strong interaction between
``colored'' objects such as quarks and gluons.
Since the model for the strong interaction is based on color, it is referred to
as Quantum Chromodynamics (QCD).
The SU(3)C group allows for singlet hadrons and color triplets of quarks,
Incorporating the covariant derivative,
|
|
| | |
¶m+igBm where Bm= |
1
2
|
llblm |
|
|
|
| (B.22) |
the locally gauge invariant Lagrangian [94] for the strong
interaction has the form
|
|
| | |
|
-
y
|
(igmDm-m)y- |
1
2
|
tr(GmnGmn) |
|
|
|
| (B.23) |
where Bm is a 3×3 matrix in color space, blm are the
eight color gauge fields (gluons) and ll are the generators of the
SU(3) gauge group.
The gluon field-strength tensor is given by
|
|
| | |
(ig)-1[Dn,Dm] = ¶nBm -¶mBn+ig[Bn,Bm] |
|
|
|
| (B.24) |
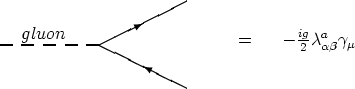
In the framework of QCD, the Feynman rule for the quark-gluon vertex in terms
of the parameters g and ll is of the form
The commutator term ig[Bn,Bm] arises from the non-Abelian nature of
the SU(3)C group.
Unlike QED, the non-Abelian nature of QCD leads to the self-couplings of the
strong gauge bosons, namely the gluons.
The Running Strong Coupling Constant, as
One important effect of the gluon self-coupling is the anti-shielding of the
vacuum polarization expected for quark-anti-quark pairs.
Unlike the QED charge screening, the QCD anti-screening of color charge results
in the decrease with increasing momentum transfer of the strong coupling
constant, as(q2), according to,
|
|
| | |
|
as(q2°)
1 + (33-2nf)as(q2°)ln(q2/q°2)/12p
|
|
|
| | |
|
|
| (B.25) |
where L2 º q2°e-1/Bas(q°2)
[91],
As long as nf £ 16, the strong coupling constant, as(q2),
increases as q2 (or r) decreases.
This phenomena is referred to as the ``running'' of as(q2).
The ``running'' of as(q2) has different implications for the two
different regimes of momentum transfer.
For low momentum transfers, as(q2) is very large preventing the
use of perturbative techniques in calculations for QCD as used in QED and leads
to the confinement of free quarks into colorless singlet state.
For large momentum transfers, as(q2)® 0 as
q2® ¥ permitting the use of perturbative techniques to be
applied to QCD calculations and resulting in ``asymptotic freedom'' of quarks.
Asymptotic freedom refers to the phenomenon of quarks to behave as if they are
free, although no quark has been observed in isolation.
Fragmentation
The process of transformation of inital quarks or gluons into more and more
partons with smaller and smaller virtual masses in the low momentum region
of as(q2) is called ``fragmentation'' or ``hadronization''.
Fragmentation occurs when an initial quark anti-quark pair separates bringing
about an increased potential energy of the color field which causes the
materialization of other quark anti-quark pairs as well as gluons which then
regroup into colorless hadrons.
At high center of mass energies these hadrons form back to back sprays of
collimated particles referred to as ``jets''.
Since perturbative QCD no longer holds at low momentum, the jets due to the
fragmentation are modelled using another approach involving fragmentation
functions.
The approach of fragmentation functions is applied to the differential
cross-section for a particular hadron, h, as follows,
|
|
| | |
|
å
q
|
s(e+e-® q |
-
q
|
)[ Dhq(z)+Dh[`(q)](z)] |
|
|
|
| (B.26) |
where z = Eh/Eq = 2Eh/s is the fraction of the quark's energy
carried by the hadron, h.
The fragmentation function is constrained to satisfy conservation of
probability and momentum as follows,
|
|
|
|
å
q
|
|
ó
õ
|
1
zmin
|
[Dhq(z)+Dhq(z)]dz |
| | |
|
|
| (B.28) |
where zmin is the threshold energy for producing the hadron of type h
and nh is the average multiplicity of hadrons of type h.
The fragmentation function Dhq(z) can be parameterized in many
different ways testimony to the large number of different Monte Carlo
generators which have been developed to model fragmentation.
One common parameterization [96] used in the independent
fragmentation picture is the following,
This parameterization agrees with the logarithmic increase in the
mean multiplicity of fragmentation with energy observed in experimentation,
i.e.
as
Eq®¥.
Another model [97] fragments the heavy quarks (c, b, t)
into hadrons which carry away relatively high fractions of the initial energy.
This model is referred to as the Peterson model and is expressed as
|
|
| | |
Kz-1 |
é
ë
|
1- |
1
z
|
- |
eQ
1-z
|
ù
û
|
-2
|
|
|
|
|
| (B.30) |
where the parameter eQ=ám2qi+p2Tqiñ/ám2Q+p2TQñ regulates the ``hardness'' of the
fragmentation function.
The Z0 Coupling to Quark Pairs
In analogy to the Z0 coupling to fermion pairs in
Subsection B, the cross-section for
s( e+e-® Z0® q[`(q)] ® hadrons) can be
expressed in terms of the cross-section of other fermions like
s( e+e-® Z0® m-m+) as,
where the sum is over all possible quark flavors, eq is the fractional
charge of the quark, and the factor of 3 is due to the different possible quark
colors.
The ratio of the cross-sections for hadrons to leptons is then given by
[91]
|
|
| | |
|
s(e+e-® hadrons)
s(e+e-®m+m-
|
= 3 |
å
q
|
eq2 |
|
|
|
| (B.32) |
Present measurements of R confirm the three colors of quarks and as a function
of the center-of-mass energy give an indication of the threshold for the
production of a new quark flavor.
Including O(as) corrections to R, yields a ~ 5% correction
which is still not yet distinguishable within present experimental errors,
|
|
| | |
3 |
å
q
|
e2q |
é
ë
|
1 + |
as(q2)
p
|
ù
û
|
|
|
|
|
| (B.33) |
Three jet events in e+e- collisions have also yielded a wealth of
information about the energy dependence of the strong interaction coupling
constant, as(q2).
The rate of three-jet events is directly proportional to as(q2) and
arises from the hadrons which fragment from an initial q[`(q)] pair and a
gluon radiated from the initial q or [`(q)].
The measured rates at Ös
= 30 GeV indicate that as @ 0.2.
At the higher center of mass energies of the LEP collider where
Ös @ 90 GeV, as has been determined to be
0.124±0.008 [18] consistent with the ``running'' of the
coupling constant.
The angular distribution of the gluon jets is also consistent with the gluon
being a spin-1 particle as required by QCD.
The Future of the Standard Model
At colliders PEP, TRISTAN and LEP, the SM has enjoyed an been very successful
in describing a large body of phenomena within the electromagnetic, the weak,
and the strong interaction across a wide range of energies as shown in
Figure B.1 [98].
However, there are a number of questions which remain unanswered by the
Standard Model theory.
Firstly, if the symmetry group SU(3)C ÄSU(2)L ÄU(1)Y
is a low energy manifestation of a broken GUT symmetry group (1014 GeV),
there will be mass corrections to the Higgs boson of
dm2 ~ g2 v21 where v1 ~ 1014 GeV.
These terms require very fine cancellations to result in a mass of order
250 GeV for the Higgs.
This problem might be resolved by rejecting the idea of symmetry breaking
induced through the Higgs mechanism or introducing more particles into the
theory to cancel the divergence.
The former is the approach of composite models which introduce symmetry
breaking through dynamical means, while the latter is the approach of
supersymmetry models.
The SM does not address why there are several families of particles and why
the connection between quarks and leptons exists, nor does the SM address the
origin of parity and CP-violation.
Finally, the SM has not yet been able to incorporated the gravitational force
into its framework, toward a unified theory of everything.
Vive les théoritiens!
Figure B.1: The e+e- Cross-section at LEP.
Measurements of e+e- cross-sections at LEP including
e+e-® (Z0) ® m+m-,
e+e-® (Z0) ® gg and
e+e-® (Z0) ® hadrons.
The measurements of e+e- cross-sections at lower energies are also shown
for CESR, DORIS, PEP, PETRA and TRISTAN.